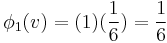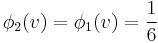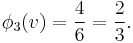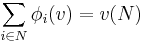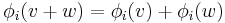Shapley value
In game theory, the Shapley value, named in honour of Lloyd Shapley, who introduced it in 1953, is a solution concept in cooperative game theory. To each cooperative game it assigns a unique distribution (among the players) of a total surplus generated by the coalition of all players. Shapley value is characterized by a collection of desirable properties or axioms described below.
The setup is as follows: a coalition of players cooperates, and obtains a certain overall gain from that cooperation. Since some players may contribute more to the coalition than others or may possess different bargaining power (for example threatening to destroy the whole surplus), what final distribution of generated surplus among the players should we expect to arise in any particular game? Or phrased differently: how important is each player to the overall cooperation, and what payoff can he reasonably expect? Shapley value provides one possible answer to this question.
Contents |
Formal definition
To formalize this situation, we use the notion of a coalitional game: we start out with a set N (of n players) and a function 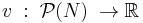 , that goes from subsets of players to reals and is called a characteristic function. We always let
, that goes from subsets of players to reals and is called a characteristic function. We always let 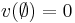 , where
, where 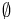 denotes the empty set.
denotes the empty set.
Function v has following meaning: if S is a coalition of players which agree to cooperate, then v(S), called the worth of coalition S, describes the total expected gain from this cooperation, independent of what the players outside of S do.
The Shapley value is one way to distribute the total gains to the players, assuming that they all collaborate. It is a "fair" distribution in the sense that it is the only distribution with certain desirable properties to be listed below. According to Shapley value the amount that player i gets given a coalitional game 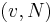 is
is
where n is the total number of players and the sum extends over all subsets S of N not containing player i. The formula can be interpreted as follows. Imagine the coalition being formed one actor at a time, with each actor demanding their contribution v(S∪{i}) − v(S) as a fair compensation, and then averaging over the possible different permutations in which the coalition can be formed.
Example
Consider a simplified description of a business. We have an owner o, who does not work but provides the crucial capital, meaning that without him no gains can be obtained. Then we have k workers w1,...,wk, each of whom contributes an amount p to the total profit. So N = {o, w1,...,wk} and v(S) = 0 if o is not a member of S and v(S) = mp if S contains the owner and m workers. Computing the Shapley value for this coalition game leads to a value of mp/2 for the owner and p/2 for each worker.
Glove game
The glove game is a coalitional game where the players have left and right hand gloves and the goal is to form pairs.
where players 1 and 2 have right hand gloves and player 3 has a left hand glove
The value function for this coalitional game is
Where the formula for calculating the Shapley value is:
Where 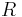 is an ordering of the players and
is an ordering of the players and 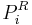 is the set of players in
is the set of players in  which precede
which precede 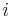 in the order
in the order 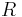
The following table displays the marginal contributions of Player 1
Order 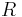 |
MC_1 |
|---|---|
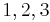 |
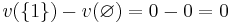 |
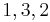 |
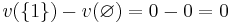 |
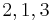 |
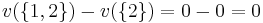 |
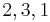 |
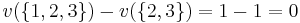 |
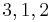 |
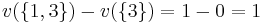 |
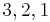 |
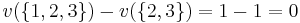 |
By a symmetry argument it can be shown that
Due to the efficiency axiom we know that the sum of all the Shapley values is equal to 1, which means that
Properties
The Shapley value has the following desirable properties:
1. Individual fairness: φi(v) ≥ v({i}) for every i in N, i.e. every actor gets at least as much as he or she would have got had they not collaborated at all.
2. Efficiency: The total gain is distributed:
3. Symmetry: If i and j are two actors who are equivalent in the sense that
for every subset S of N which contains neither i nor j, then φi(v) = φj(v).
4. Additivity: if we combine two coalition games described by gain functions v and w, then the distributed gains should correspond to the gains derived from v and the gains derived from w:
for every i in N.
5. Zero Player (Null player): A null player should receive zero. A player  is null if
is null if 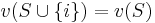 for all
for all  not containing
not containing  .
.
In fact, given a player set N, and payout (reward) function v(S), the vector of Shapley values is the only vector, defined on the class of all superadditive games that satisfies all four properties 2, 3, 4 and 5 from above.
Addendum definitions
1. Anonymous: If i and j are two actors, and w is the gain function that acts just like v except that the roles of i and j have been exchanged, then φi(v) = φj(w). In essence, this means that the labeling of the actors doesn't play a role in the assignment of their gains. Such a function is said to be anonymous.
2. Marginalism: the Shapley value can be defined as a function which uses only the marginal contributions of player i as the arguments.
Aumann–Shapley value
In their 1974 book, Shapley and Robert Aumann extended the concept of the Shapley value to infinite games (defined with respect to a non-atomic measure).
See also
References
- Lloyd S. Shapley. "A Value for n-person Games". In Contributions to the Theory of Games, volume II, by H.W. Kuhn and A.W. Tucker, editors. Annals of Mathematical Studies v. 28, pp. 307–317. Princeton University Press, 1953.
- Robert J. Aumann, Lloyd S. Shapley. Values of non-atomic games, Princeton Univ. Press, Pinceton, 1974.
- Alvin E. Roth (editor). The Shapley value, essays in honor of Lloyd S. Shapley. Cambridge University Press, Cambridge, 1988.
- Sergiu Hart, Shapley Value, The New Palgrave: Game Theory, J. Eatwell, M. Milgate and P. Newman (Editors), Norton, pp.210–216, 1989.
External links
- [1] – A Bibliography of Cooperative Games: Value Theory by Sergiu Hart
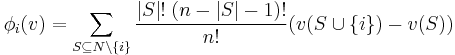
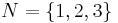
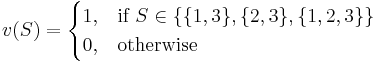
![\phi_i(v)= \frac{1}{|N|!}\sum_R\left [ v(P_i^R \cup \left \{ i \right \}) - v(P_i^R) \right ]\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/90b5f653b5f9312fd086eefa26b9fd7c.png)